函数对称性是高中数学中的一个重要概念，它涉及到函数图像关于坐标轴的对称性质。在解题过程中，掌握函数对称性公式能够帮助我们简化计算，并且更好地理解和应用函数的特点。本文将从函数对称性的定义和性质出发，常见的函数对称性公式，并探讨其在高中数学中的应用。

一、关于x轴对称的函数（1个段落）

函数关于x轴对称意味着函数图像在x轴上具有对称性。利用x轴对称性公式，我们可以通过一个已知点得出对称点的坐标，并且在解题过程中可以简化计算。

二、关于y轴对称的函数（1个段落）

函数关于y轴对称意味着函数图像在y轴上具有对称性。利用y轴对称性公式，我们可以通过一个已知点得出对称点的坐标，并且在解题过程中可以简化计算。

三、关于原点对称的函数（1个段落）

函数关于原点对称意味着函数图像在原点具有对称性。利用原点对称性公式，我们可以通过一个已知点得出对称点的坐标，并且在解题过程中可以简化计算。

四、关于直线y=x对称的函数（1个段落）

函数关于直线y=x对称意味着函数图像在直线y=x上具有对称性。利用直线y=x对称性公式，我们可以通过一个已知点得出对称点的坐标，并且在解题过程中可以简化计算。

五、关于直线y=-x对称的函数（1个段落）

函数关于直线y=-x对称意味着函数图像在直线y=-x上具有对称性。利用直线y=-x对称性公式，我们可以通过一个已知点得出对称点的坐标，并且在解题过程中可以简化计算。

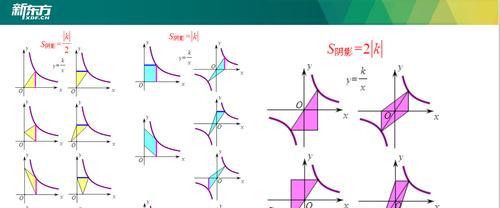
六、关于垂直于x轴的直线对称的函数（1个段落）

函数关于垂直于x轴的直线对称意味着函数图像在垂直于x轴的直线上具有对称性。利用垂直于x轴的直线对称性公式，我们可以通过一个已知点得出对称点的坐标，并且在解题过程中可以简化计算。

七、关于垂直于y轴的直线对称的函数（1个段落）

函数关于垂直于y轴的直线对称意味着函数图像在垂直于y轴的直线上具有对称性。利用垂直于y轴的直线对称性公式，我们可以通过一个已知点得出对称点的坐标，并且在解题过程中可以简化计算。

八、奇函数和偶函数（1个段落）

奇函数和偶函数是函数对称性的两种特殊情况。奇函数关于原点对称，而偶函数关于y轴对称。我们可以利用奇偶函数的性质进行简化计算和推导。

九、应用一：解二次方程（1个段落）

通过运用函数对称性公式，我们可以简化解二次方程的过程。将二次方程表示成关于x轴对称、y轴对称或原点对称的函数形式，可以帮助我们更好地理解解的过程。

十、应用二：求解函数的零点（1个段落）

利用函数对称性公式，我们可以通过已知零点得出对称零点的坐标，并且在解题过程中可以简化计算。

十一、应用三：求解函数的最值（1个段落）

通过运用函数对称性公式，我们可以通过已知最值点得出对称最值点的坐标，并且在解题过程中可以简化计算。

十二、应用四：图像变换（1个段落）

通过运用函数对称性公式，我们可以在不进行具体计算的情况下，得到函数图像关于坐标轴进行平移、翻转等变换后的性质。

十三、应用五：解题技巧（1个段落）

掌握函数对称性公式，可以帮助我们在解题过程中更快地得出结论或者简化计算，提高解题效率。

十四、拓展与应用领域（1个段落）

函数对称性公式不仅在数学中有广泛应用，也可以在物理、工程等领域中发挥重要作用。进一步了解函数对称性的应用领域，可以更好地理解其实际意义。

十五、（1个段落）

通过本文的介绍，我们对高中函数对称性公式有了更全面的认识。掌握这些公式可以帮助我们更好地理解和应用函数的特点，在解题过程中提高效率，拓展应用领域。