方差是统计学中常用的一种测量数据变异程度的指标,它能够帮助我们了解数据集的分散程度和集中趋势。在Excel中,我们可以通过一系列的计算公式和函数来方便地计算方差,并利用这些结果进行更深入的数据分析和决策。本文将从理论和实际应用的角度,探讨方差的计算原理以及如何在Excel中使用相应的公式进行分析。
一什么是方差
方差是统计学中最常用的描述数据分散程度的指标之一。它可以反映出一组数据与其平均值之间的偏离程度。方差越大,意味着数据点离平均值越远,数据分布越分散;而方差越小,则表示数据点相对集中,分布趋于一致。
二总体方差与样本方差
在统计学中,我们常常需要区分总体方差和样本方差。总体方差用于描述整个数据集的分散程度,而样本方差仅仅是总体方差的估计值,用于从样本数据推断总体数据的特征。
三方差计算公式
方差的计算公式基于数据与平均值之间的差异,通常使用平方差的平均值来作为方差的估计。在Excel中,我们可以使用VAR.P和VAR.S函数来计算总体方差和样本方差。VAR.P代表总体方差,VAR.S代表样本方差。
四总体方差的计算方法
总体方差的计算方法较为简单。我们可以通过计算每个数据点与总体均值之间的平方差,然后求这些平方差的平均值得到总体方差。在Excel中,使用VAR.P函数可以直接计算总体方差。
五样本方差的计算方法
样本方差的计算方法与总体方差类似,只是在计算平均值时使用样本均值代替总体均值。在Excel中,我们可以使用VAR.S函数来计算样本方差。

六样本方差的偏倚修正
由于样本方差使用样本均值估计总体均值,所以会存在一定的偏差。为了消除这种偏差,可以使用修正的样本方差计算公式,即除以样本大小减1。在Excel中,我们可以通过STDEVP和STDEV.S函数来计算标准差,然后再平方得到修正的样本方差。
七Excel中方差计算函数的使用
Excel提供了多个方差计算函数,如VAR.P、VAR.S、STDEVP和STDEV.S等。通过合理地运用这些函数,我们可以方便地计算总体和样本方差,并快速获得结果。
八方差的应用举例
方差的计算结果可以帮助我们了解数据的分布情况,并从中获取有关数据集的有用信息。在金融领域,方差可以帮助我们评估投资组合的风险;在制造业中,方差可以帮助我们分析产品质量的稳定性。
九方差与协方差的关系
方差与协方差密切相关。协方差衡量了两个随机变量之间的相关性,而方差是协方差的一种特殊情况,即一个变量与自身的协方差。
十方差分析的应用
方差分析是一种常用的统计方法,用于比较不同样本之间的差异。通过计算不同组之间的方差和内部组之间的方差,我们可以判断不同组之间的差异是否显著。
十一Excel中方差分析的实现
在Excel中,我们可以利用内置的方差分析工具,如ANOVA函数,来快速进行方差分析。通过简单的操作,我们可以得到关于不同组之间差异的统计结果。
十二常见误区与注意事项
在使用方差计算公式和Excel函数进行分析时,需要注意一些常见的误区,如样本大小、数据类型和数据范围等。只有合理地处理这些问题,才能得到准确可靠的结果。
十三方差计算公式的局限性
尽管方差是一种常用的统计指标,但它也存在一定的局限性。方差只能反映数据的分散程度,并不能提供有关数据分布形状和异常值的信息。
十四其他常用统计指标
除了方差之外,统计学中还有许多其他常用的指标,如标准差、平均值等。这些指标可以与方差结合使用,提供更全面的数据分析结果。
十五
通过本文的介绍,我们了解了方差的计算公式和Excel函数的应用方法,并探讨了方差在数据分析中的重要性和局限性。方差作为一种常用的统计指标,在数据分析和决策中发挥着重要作用。希望本文能够帮助读者更好地理解和应用方差计算公式。
利用Excel计算方差的公式分析
在进行数据分析和统计时,方差是一个重要的概念。它可以帮助我们了解数据的离散程度和变异程度。利用Excel的方差计算公式,我们可以快速准确地得出数据集的方差,并进一步分析数据的特征和趋势。本文将详细介绍如何使用Excel计算方差的公式,并通过实例演示其实际应用。
什么是方差及其作用
方差是统计学中用来衡量一组数据的离散程度的指标。它可以告诉我们数据点相对于其平均值的分散程度,即数据集内部的变异程度。方差越大,数据点间的差异越大;方差越小,数据点间的差异越小。在数据分析中,我们常常使用方差来比较不同数据集的离散程度,并从中得出结论。
Excel中方差计算公式的基本原理
在Excel中,方差的计算公式基于样本方差(s^2)或总体方差(σ^2)。对于样本方差,公式为=sum((x-x?)^2)/(n-1),其中x为数据集中的每个数据点,x?为数据集的平均值,n为数据集的样本个数。对于总体方差,公式为=sum((x-x?)^2)/n,其中n为数据集的总体个数。通过在Excel中使用这些公式,我们可以轻松计算出方差。
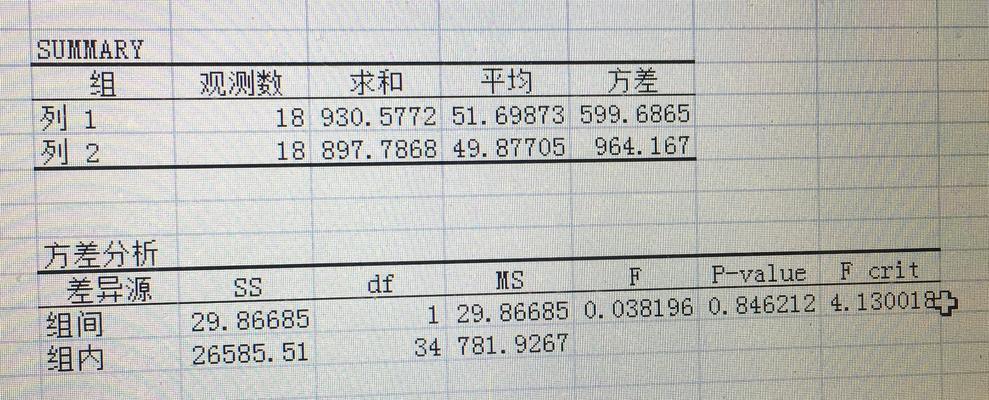
在Excel中使用样本方差函数计算方差
Excel提供了多种函数用于计算方差。样本方差函数VAR.S是最常用的函数之一。使用VAR.S函数,我们只需选中数据集范围,然后在函数栏中输入“=VAR.S(数据范围)”,即可得到样本方差的计算结果。VAR.S函数会自动忽略文本和空白单元格,并将计算结果返回。
在Excel中使用总体方差函数计算方差
如果我们需要计算总体方差,可以使用VAR.P函数。与VAR.S函数类似,只需选中数据集范围,然后在函数栏中输入“=VAR.P(数据范围)”,即可得到总体方差的计算结果。VAR.P函数同样会自动忽略文本和空白单元格,并返回计算结果。
使用Excel的数据分析工具包计算方差
除了上述函数外,Excel还提供了数据分析工具包,其中包含了更多的统计函数和工具。我们可以通过加载数据分析工具包,使用工具包中的方差函数进行计算。使用数据分析工具包,我们可以更加灵活地选择计算方差时所采用的方法,并可以进行更多的统计分析。
方差计算结果的解读
一旦我们得到了方差的计算结果,就可以对数据集的特征和趋势进行进一步的分析和解读。较大的方差表示数据的分散程度较大,可能存在较大的波动性或差异性。而较小的方差则表示数据的分散程度较小,数据点间的差异较小。通过方差的计算结果,我们可以得出有关数据集分布、离散程度和稳定性的结论。
方差计算中的常见问题与解决办法
在使用Excel进行方差计算时,可能会遇到一些常见问题,如数据范围选择不准确、函数使用错误等。针对这些问题,我们可以采取一些解决办法,如仔细检查数据范围、检查函数输入是否正确等。通过熟练掌握方差计算的方法和技巧,我们可以更好地应对这些问题。
方差计算的实例演示1
为了更好地理解方差计算的过程和方法,我们以一个具体的实例来进行演示。假设有一组销售数据,我们想要计算该数据集的方差。我们需要选中数据集范围,然后使用VAR.S或VAR.P函数进行计算。我们可以根据计算结果对数据集进行分析和解读。
方差计算的实例演示2
继续上述实例,我们可以进一步展示如何使用Excel的数据分析工具包进行方差计算。通过加载工具包,并选择合适的方差函数,我们可以得到与前述方法相同的结果。演示过程中还将介绍如何解读计算结果,并给出一些建议和结论。
方差计算在数据分析中的应用
方差是数据分析中常用的统计指标之一,广泛应用于金融、市场研究、质量控制等领域。通过计算方差,我们可以对数据集的波动性、稳定性和风险进行评估,并基于评估结果做出相应的决策和调整。掌握方差计算的方法,可以帮助我们更好地理解和分析数据。
方差计算的局限性与注意事项
尽管方差是一种有用的统计指标,但在使用时也需要注意其局限性和适用范围。方差对异常值敏感,且不易对非正态分布的数据进行准确的度量。在比较多个数据集时,还需要考虑样本量和数据来源的差异等因素。在进行方差计算时,需要综合考虑多个因素,并结合其他统计方法进行分析。
学习Excel方差计算的其他资源
除了本文介绍的方差计算方法外,还有许多其他资源可以帮助我们更深入地学习和理解Excel中的方差计算。可以通过参考相关书籍、在线教程或参加培训课程来进一步提升自己的技能和知识。通过不断学习和实践,我们可以更好地掌握方差计算方法,并在数据分析中取得更好的效果。
Excel方差计算的重要性和应用价值
方差作为一种重要的统计指标,在数据分析中具有广泛的应用价值。通过利用Excel的方差计算公式,我们可以快速准确地得出数据集的方差,并进一步分析数据的特征和趋势。熟练掌握方差计算的方法和技巧,可以提高我们的数据分析能力,并帮助我们做出更准确的决策。
本文详细介绍了利用Excel计算方差的公式分析的方法和步骤。通过学习和掌握这些知识,我们可以在数据分析和统计中更好地使用方差这一重要指标,并能够对数据的离散程度和变异程度进行准确评估。通过不断实践和应用,我们可以在数据分析领域取得更好的成果。