数学作为一门科学，其各个分支都有其独特的公式和定理。在高中数学中，双曲线公式是一个重要的内容。本文将深入探讨双曲线的公式、特性以及应用，帮助读者更好地理解和运用双曲线公式解决实际问题。

1.双曲线的定义及基本特性

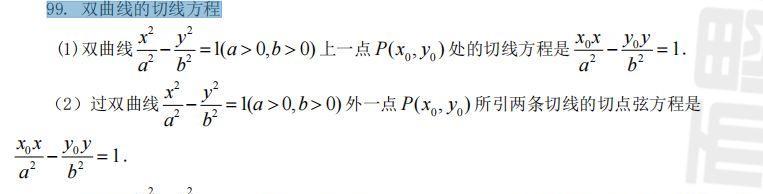
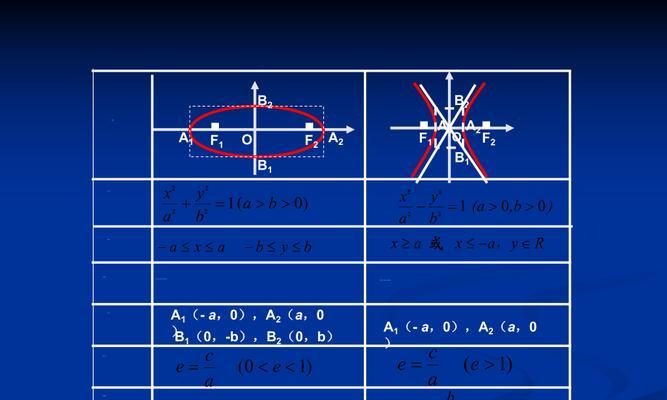
双曲线是二次曲线的一种，其特点是两个分离的非交叉的曲线分支。它可以通过一个常数e来定义，其中e>1表示双曲线打开方向在y轴上，e<1表示双曲线打开方向在x轴上。

2.双曲线的标准方程

双曲线的标准方程为x^2/a^2-y^2/b^2=1，其中a和b是正实数。通过标准方程，我们可以得到双曲线的中心、焦点、顶点等重要信息。

3.双曲线的焦点和直角坐标系

双曲线的焦点是双曲线上到两个分支距离和为定值的点。在直角坐标系中，可以通过求焦点坐标的方法来确定双曲线的位置和形状。

4.双曲线的渐近线

双曲线有两条渐近线，分别与双曲线的两个分支趋于无穷远。这些渐近线可以帮助我们更好地理解双曲线的形态和性质。

5.双曲线的离心率

双曲线的离心率是描述其形状的重要参数，它决定了双曲线的开口大小和曲线的扁平程度。离心率越大，双曲线的开口越大；离心率越小，双曲线的开口越小。

6.双曲线在物理学中的应用

双曲线在物理学中有广泛的应用，尤其是在电磁场、声波传播、天体运动等领域。通过双曲线公式和双曲线的特性，我们可以更好地描述和解释这些自然现象。

7.双曲线在经济学中的应用

双曲线也被广泛应用于经济学中的供需关系、消费模型、金融市场等领域。通过双曲线的形状和方程，我们可以分析和预测经济变量的变化趋势。

8.双曲线在工程中的应用

双曲线在工程学中有许多应用，例如天桥的设计、通信信号的传输、力学系统的分析等。通过双曲线的公式和特性，工程师可以更好地设计和优化各种系统。

9.双曲线与其他数学概念的联系

双曲线与其他数学概念存在着密切的联系，例如椭圆、抛物线、直线等。通过比较和对比，我们可以更好地理解和运用双曲线公式解决问题。

10.双曲线公式的变形与推广

双曲线公式可以进行变形和推广，例如通过平移、旋转等操作来获得新的双曲线方程。这些变形和推广可以帮助我们更灵活地运用双曲线公式解决实际问题。

11.双曲线与数学建模

双曲线在数学建模中起到重要的作用，可以帮助我们描述和预测各种实际问题。通过建立适当的数学模型，我们可以利用双曲线公式来解决实际问题并做出决策。

12.双曲线公式的证明与推导

双曲线公式的证明和推导是数学研究中的重要内容，通过推导我们可以更深入地理解双曲线的性质和特点。

13.双曲线的应用举例：天体轨道

双曲线在天体运动中的应用是一个重要的例子。通过双曲线公式，我们可以描述和预测彗星、行星等天体的轨道运动。

14.双曲线的应用举例：信号传输

双曲线在通信领域中的应用也是一个重要的例子。通过双曲线的形状和方程，我们可以优化信号传输系统，提高通信质量。

15.双曲线公式的实际应用挑战与解决

双曲线公式在实际应用中可能会遇到一些挑战，例如参数的确定、误差的估计等。我们需要通过数学方法和实际数据来解决这些问题，使双曲线公式更好地适应实际情况。

通过对高中数学双曲线公式的全面和应用，我们可以更好地理解双曲线的特性和应用。双曲线公式作为数学中的重要内容，不仅在理论研究中有广泛应用，也在各个学科和领域中发挥着重要作用。希望本文对读者对双曲线公式的理解和应用提供了一定的帮助。