广泛应用于物理学、拓扑结构是一门研究空间形态和关系的学科，计算机科学等领域，数学。并介绍其在不同领域的应用，本文将探索拓扑结构的多种类型。

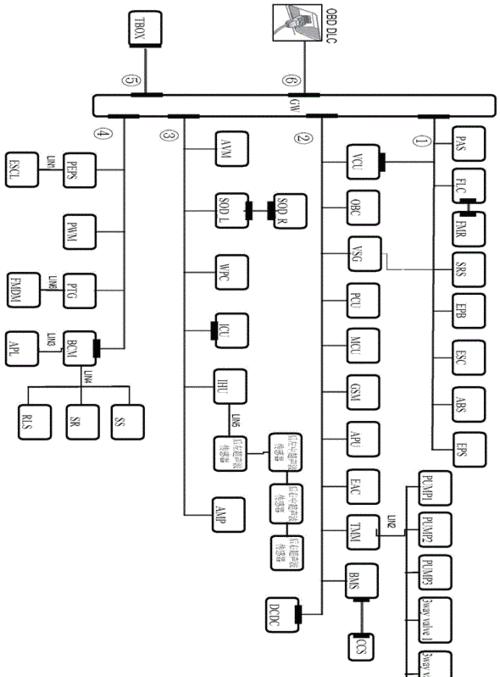
1.点集拓扑结构的基本概念与特征

用于描述中元素之间的连接方式和性质，由点和它们之间的关系组成、点集拓扑结构是最基础的拓扑结构类型。

2.线性拓扑结构及其在物理学中的应用

常用于表示线性排列的元素和它们之间的顺序关系，线性拓扑结构是由一条直线上的点和它们之间的关系组成，在物理学中有广泛应用。

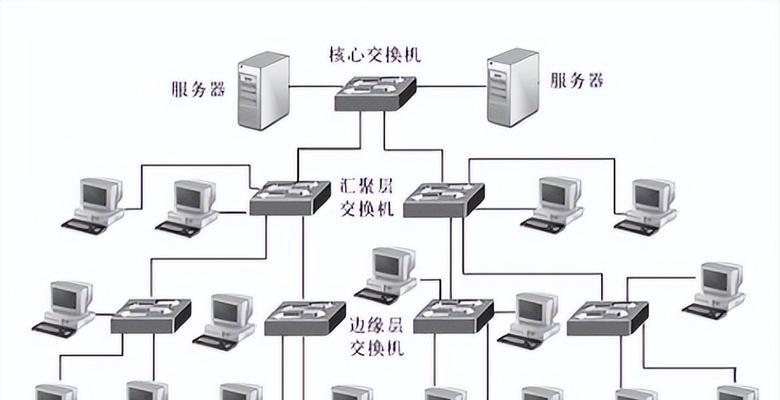
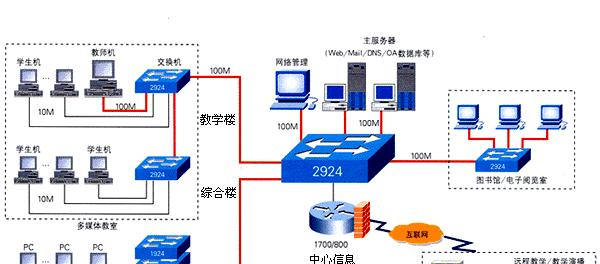
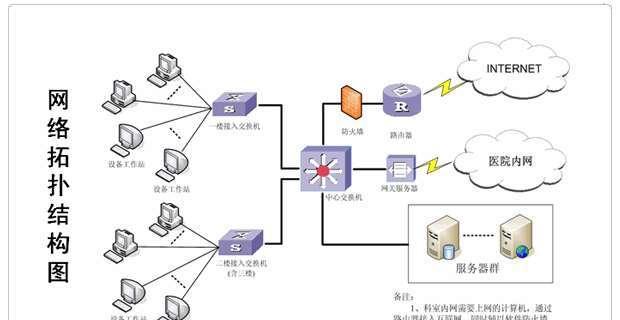
3.网状拓扑结构及其在计算机网络中的应用

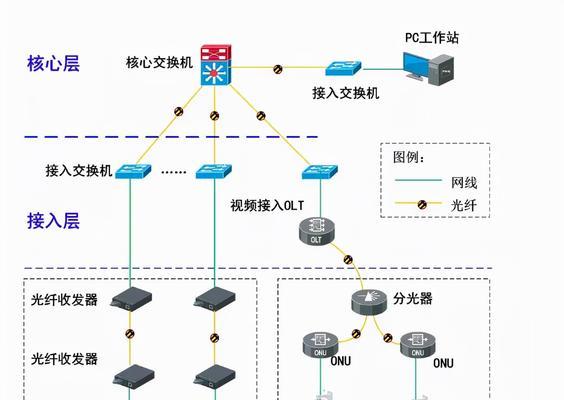
如计算机网络中的多个节点之间的连接方式、常用于表示复杂的网络关系，网状拓扑结构是由多个节点通过连接线相互连接而成。

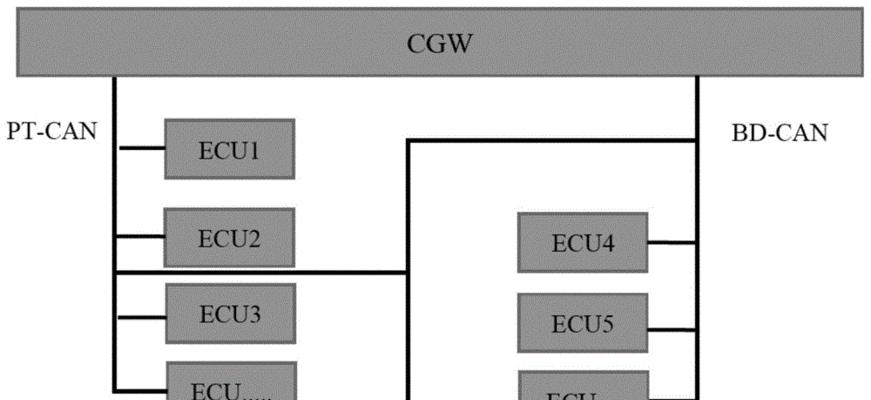
4.树状拓扑结构及其在数据结构中的应用

如树形数据结构中的父子节点关系，常用于表示数据之间的层次关系，树状拓扑结构是一种具有层次结构的拓扑结构。

5.网格拓扑结构及其在计算机图形学中的应用

常用于表示二维或三维图形中的离散点和它们之间的连接关系，网格拓扑结构是由多个网格点和网格边相互连接而成、在计算机图形学中有重要应用。

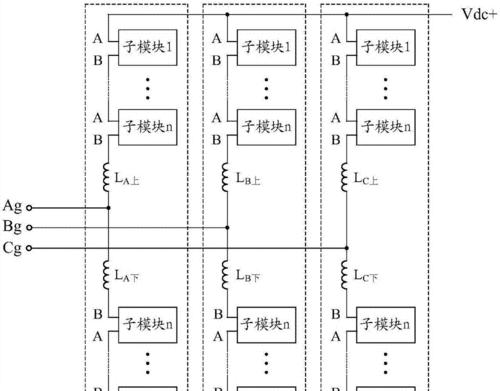
6.嵌入式拓扑结构及其在电路设计中的应用

常用于电路设计中的电子元件之间的连接关系，嵌入式拓扑结构是将一个拓扑结构嵌入到另一个拓扑结构中。

7.曲面拓扑结构及其在几何学中的应用

常用于表示曲面形状和它们之间的关系、曲面拓扑结构是由多个曲面点和曲面边相互连接而成，在几何学研究中具有重要意义。

8.流形拓扑结构及其在物理学中的应用

常用于描述空间的形状和性质，流形拓扑结构是一种具有特定性质的拓扑结构，在物理学中有广泛应用。

9.非欧几何拓扑结构及其在相对论中的应用

常用于描述相对论中的非欧空间，非欧几何拓扑结构是一种非传统的拓扑结构，对于理解相对论的几何概念具有重要意义。

10.异构拓扑结构及其在计算机科学中的应用

如分布式计算系统中的节点和连接方式、常用于表示复杂的计算机系统或网络结构，异构拓扑结构是由多个不同类型的拓扑结构组成。

11.拓扑结构在数据分析中的应用及局限性

如数据聚类，图像处理等，探讨拓扑结构在数据分析领域的应用，并讨论其应用中可能存在的局限性。

12.拓扑结构在城市规划中的应用及挑战

如交通网络规划，城市布局等，并探讨其应用过程中可能面临的挑战、分析拓扑结构在城市规划中的应用。

13.拓扑结构在生物学中的应用及发展趋势

基因调控网络分析等、探讨拓扑结构在生物学领域的应用，并展望其未来的发展趋势，如蛋白质结构预测。

14.拓扑结构在社交网络中的应用及影响

如社交关系网络、信息传播等，分析拓扑结构在社交网络分析中的应用，并讨论其对社交网络行为和社会影响的影响。

15.与展望

并展望拓扑结构在未来的研究和应用中可能带来的创新和突破、各种拓扑结构的特点和应用领域。

流形，非欧几何，从点集，异构等角度进行了详细介绍，曲面、本文深入探索了拓扑结构的多种类型，树状，嵌入式、网格，线性、网状。数据分析、同时，还介绍了拓扑结构在物理学，城市规划、生物学和社交网络等多个领域的应用，计算机科学。推动各个领域的发展和创新，通过对拓扑结构的研究和应用、我们可以更好地理解空间形态和关系。